The Riemann Hypothesis
Mathematics' greatest mystery unveiled
Introduction
One of the most profound and unsolved problems in mathematics is the Riemann Hypothesis. It lies at the heart of analytic number theory and is deeply connected to the distribution of prime numbers.
Despite being proposed in 1859, it remains unproven and continues to challenge mathematicians worldwide.
The Riemann Zeta Function
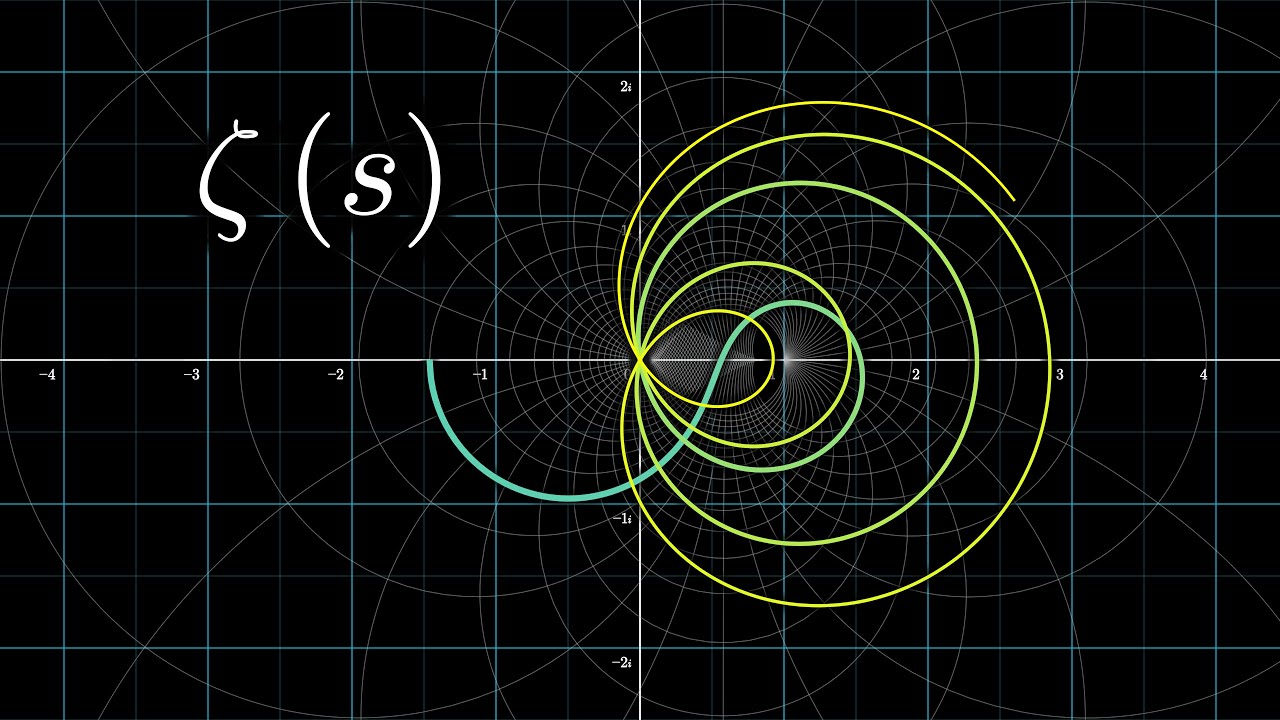
The Riemann Zeta function is a mathematical function denoted by the Greek letter ζ (zeta).
It is defined for a complex variable s as:
Where: • s can be a real or complex number • The series converges when Re(s) > 1
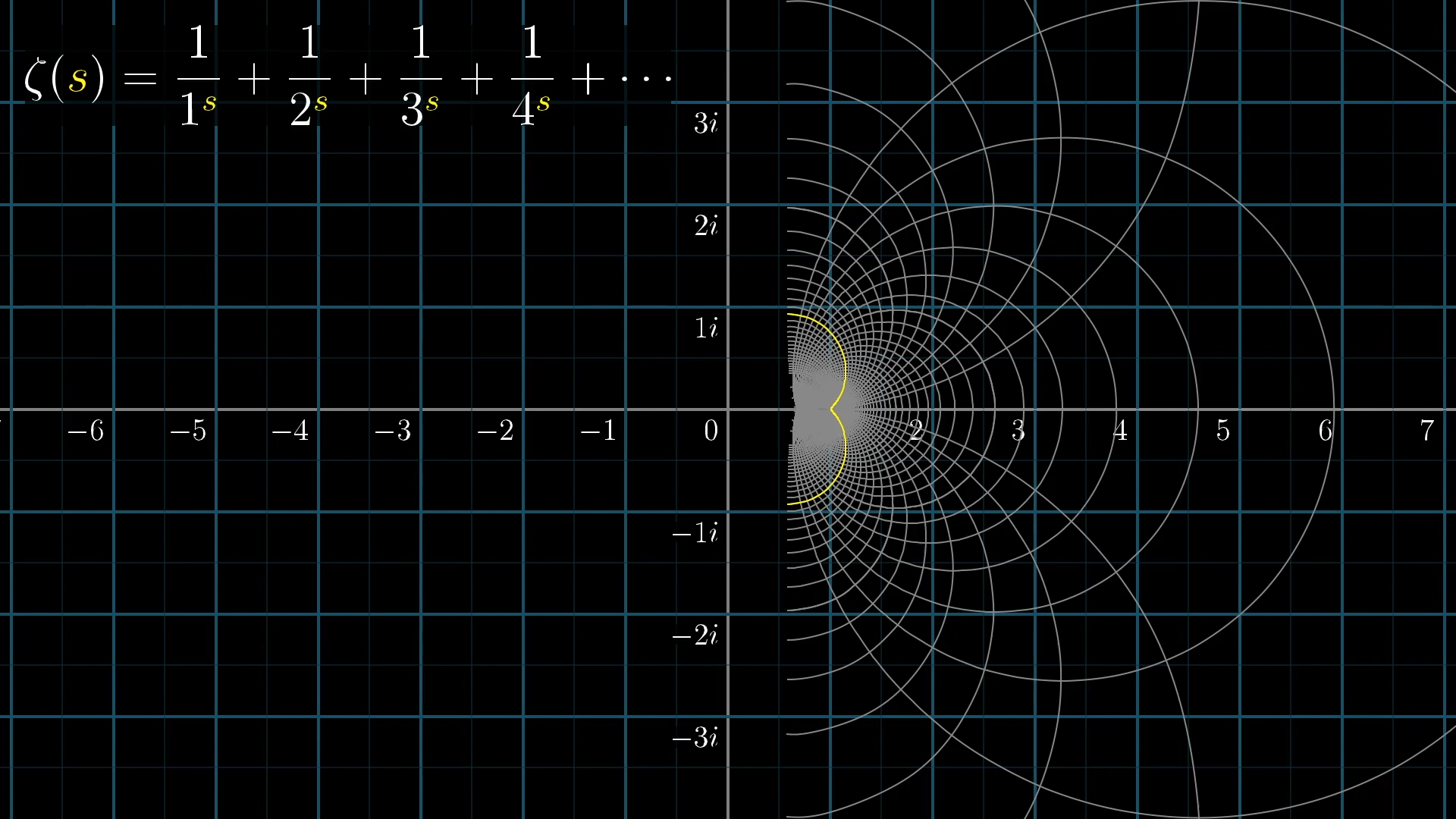
Applications of the Zeta Function
The Riemann Zeta function appears in several areas of science and mathematics, including:
- Physics
- Probability theory
- Applied statistics
- Quantum mechanics
- Chaos theory
Historical Background
The zeta function was first studied by Leonhard Euler in the 18th century, but only for real values of s.
In 1859, Bernhard Riemann extended the function to the complex plane in his paper:
*On the Number of Primes Less Than a Given Magnitude*
This extension revealed a deep relationship between the zeta function and the distribution of prime numbers.

Zeros of the Zeta Function
Trivial Zeros,
Riemann showed that when s is a negative even integer, the zeta function equals zero:
These are known as trivial zeros.
Non-Trivial Zeros
Apart from trivial zeros, the zeta function also has zeros at complex values of s.
Riemann observed that all known non-trivial zeros appeared to satisfy:
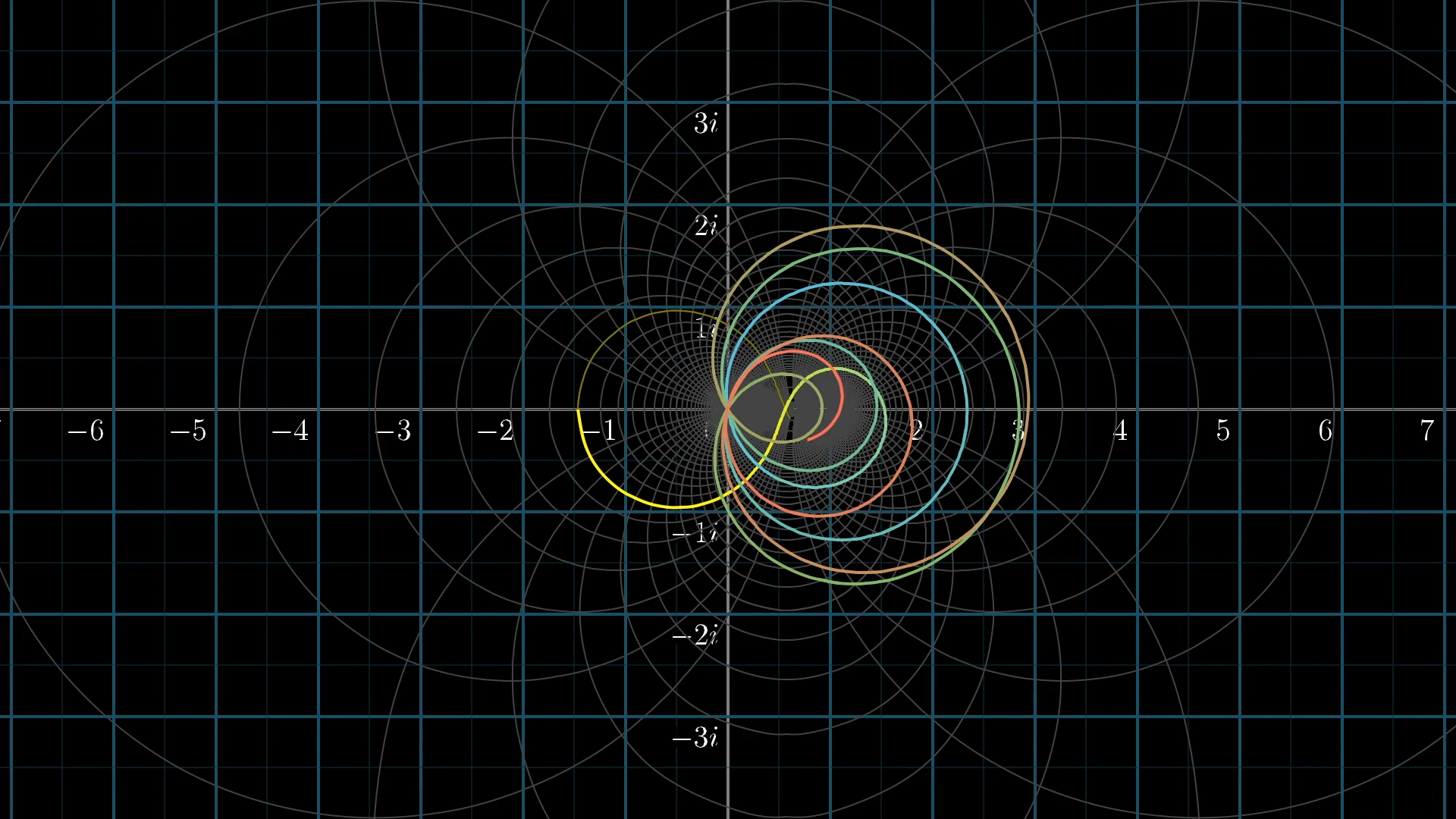
The Riemann Hypothesis
The Riemann Hypothesis states:
All non-trivial zeros of the Riemann Zeta function lie on the critical line
Mathematically, this means every non-trivial zero can be written as:
Where: • t ∈ ℝ (real numbers) • i = √(-1)
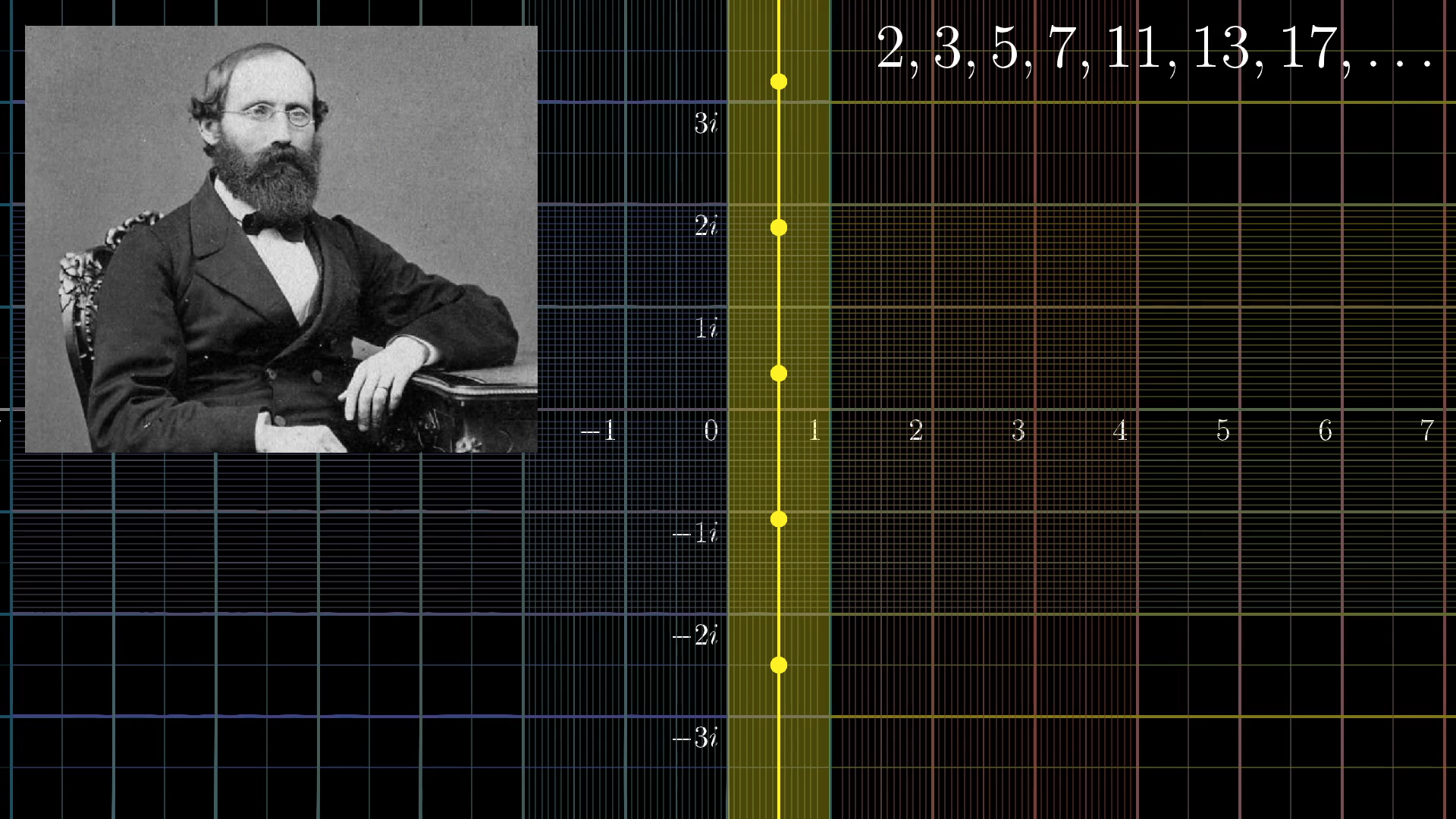
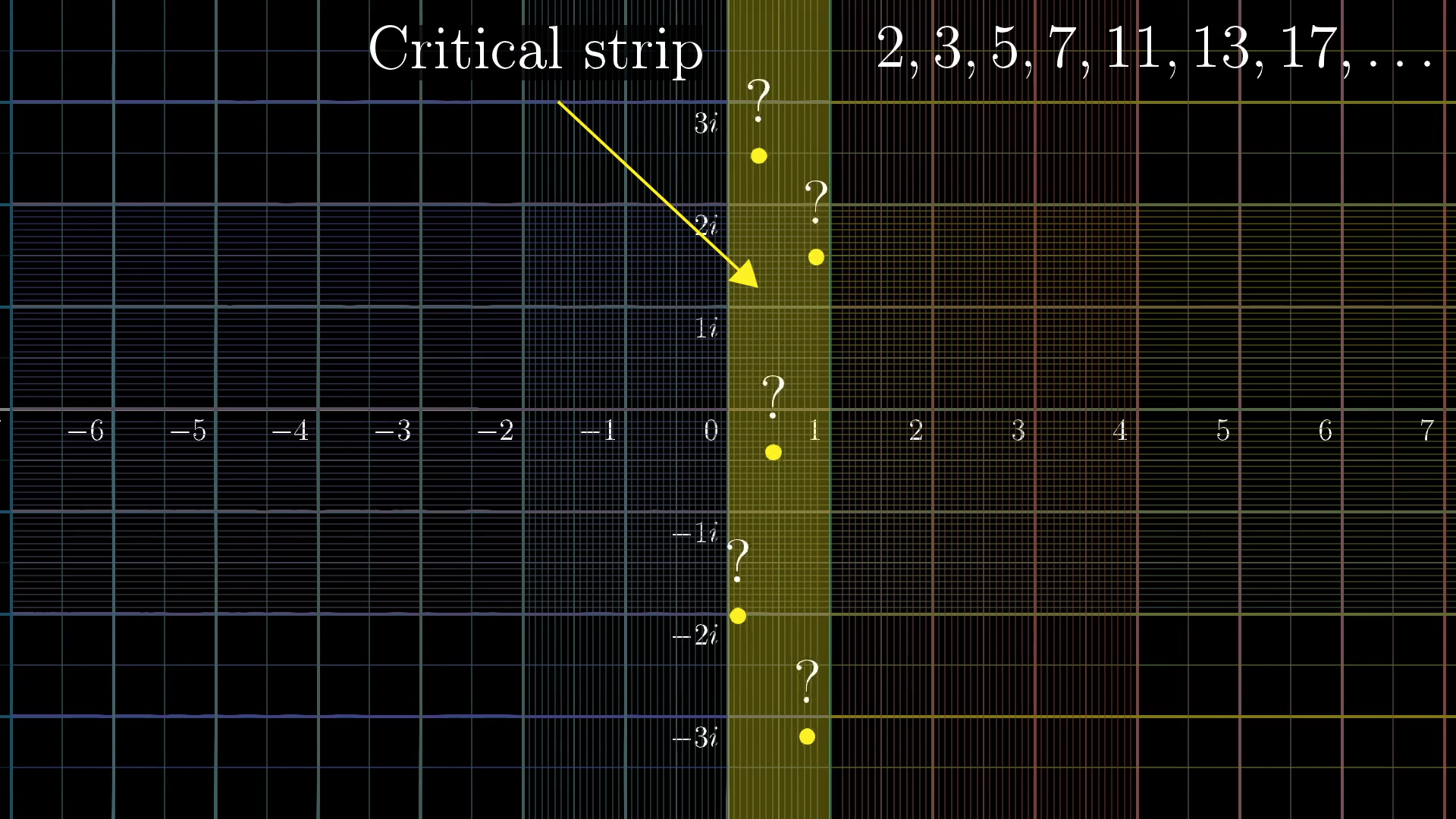
The Critical Strip and Critical Line
The critical strip is defined as:
The critical line lies at the center of this strip:
If the hypothesis is true, every non-trivial zero lies on this line.
Why the Riemann Hypothesis Matters
If proven true, the Riemann Hypothesis would:
- Reveal deep truths about the <strong class='text-white'>distribution of prime numbers</strong>
- Improve error bounds in prime-counting functions
- Impact cryptography, number theory, and mathematical physics
Because of its importance, it is one of the Clay Mathematics Institute Millennium Prize Problems, carrying a reward of:
Conclusion
The Riemann Hypothesis is simple to state but extraordinarily difficult to prove. It represents one of the deepest links between complex analysis and number theory.
More than a century later, it remains one of the greatest unsolved problems in mathematics.
Credits to 3Blue1Brown for the images